9.5: Substituted Cyclohexanes
After completing this section, you should be able to
- account for the greater stability of the equatorial conformers of monosubstituted cyclohexanes compared to their axial counterparts, using the concept of 1,3‑diaxial interaction.
- compare the gauche interactions in butane with the 1,3‑diaxial interactions in the axial conformer of methylcyclohexane.
- arrange a given list of substituents in increasing or decreasing order of 1,3‑diaxial interactions.
Make certain that you can define, and use in context, the key term below.
- 1,3‑diaxial interaction
1,3-Diaxial interactions are steric interactions between an axial substituent located on carbon atom 1 of a cyclohexane ring and the hydrogen atoms (or other substituents) located on carbon atoms 3 and 5.
Be prepared to draw Newman-type projections for cyclohexane derivatives as the one shown for methylcyclohexane. Note that this is similar to the Newman projections from chapter 3 such as n-butane.
Newman projections of methylcyclohexane and n‑butane
When a substituent is added to a cyclohexane ring, the two possible chair conformations created during a ring flip are not equally stable. In the example of methylcyclohexane the conformation where the methyl group is in the equatorial position is more stable than the axial conformation by 7.6 kJ/mol at 25o C. The percentages of the two different conformations at equilibrium can be determined by solving the following equation for K (the equilibrium constant): ΔE = -RTlnK. In this equation ΔE is the energy difference between the two conformations, R is the gas constant (8.314 J/mol•K), T is the temperature in Kelvin, and K is the equilibrium constant for the ring flip conversion. Using this equation, we can calculate a K value of 21 which means about 95% methylcyclohexane molecules have the methyl group in the equatorial position at 25o C.
The energy difference between the two conformations comes from strain, called 1,3-diaxial interactions, created when the axial methyl group experiences steric crowding with the two axial hydrogens located on the same side of the cyclohexane ring. Because axial bonds are parallel to each other, substituents larger than hydrogen experience greater steric crowding when they are oriented axial rather than equatorial. Consequently, substituted cyclohexanes will preferentially adopt conformations in which the larger substituents are in the equatorial orientation. When the methyl group is in the equatorial position this strain is not present which makes the equatorial conformer more stable and favored in the ring flip equilibrium.
Actually, 1,3-diaxial steric strain is directly related to the steric strain created in the gauche conformer of butane discussed in Section: 3-7. When butane is in the gauche conformation 3.8 kJ/mol of strain was created due the steric crowding of two methyl group with a 60o dihedral angle. When looking at the a Newman projection of axial methylcyclohexane the methyl group is at a 60o dihedral angle with the ring carbon in the rear. This creates roughly the same amount of steric strain as the gauche conformer of butante. Given that there is actually two such interactions in axial methylcyclohexane, it makes sense that there is 2(3.8 kJ/mol) = 7.6 kJ/mol of steric strain in this conformation. The Newman projection of equatorial methylcyclohexane shows no such interactions and is therefore more stable.
Newman projections of methyl cyclohexane and butane showing similarity of 1,3-diaxial and gauche interactions.
Strain values for other cyclohexane substituents can also be considered. The relative steric hindrance experienced by different substituent groups oriented in an axial versus equatorial location on cyclohexane determined the amount of strain generated. The strain generated can be used to evaluate the relative tendency of substituents to exist in an equatorial or axial location. Looking at the energy values in this table, it is clear that as the size of the substituent increases, the 1,3-diaxial energy tends to increase, also. Note that it is the size and not the molecular weight of the group that is important. Table 4.7.1 summarizes some of these strain values values.
| Substituent | –ΔG° (kcal/mol) | Substituent | –ΔG° (kcal/mol) |
| [latex]\ce{CH_3\bond{-}}[/latex] | 1.7 | [latex]\ce{O_2N\bond{-}}[/latex] | 1.1 |
| [latex]\ce{CH_2H_5\bond{-}}[/latex] | 1.8 | [latex]\ce{N#C\bond{-}}[/latex] | 0.2 |
| [latex]\ce{(CH_3)_2CH\bond{-}}[/latex] | 2.2 | [latex]\ce{CH_3O\bond{-}}[/latex] | 0.5 |
| [latex]\ce{(CH_3)_3C\bond{-}}[/latex] | [latex]\geq 5.0[/latex] | [latex]\ce{HO_2C\bond{-}}[/latex] | 0.7 |
| [latex]\ce{F\bond{-}}[/latex] | 0.3 | [latex]\ce{H_2C=CH\bond{-}}[/latex] | 1.3 |
| [latex]\ce{Cl\bond{-}}[/latex] | 0.5 | [latex]\ce{C_6H_5\bond{-}}[/latex] | 3.0 |
| [latex]\ce{Br\bond{-}}[/latex] | 0.5 | ||
| [latex]\ce{I\bond{-}}[/latex] | 0.5 |
Exercises
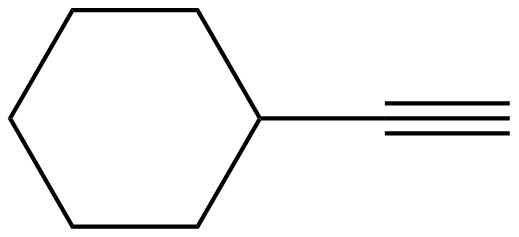
1) In the molecule, cyclohexyl ethyne there is little steric strain, why?
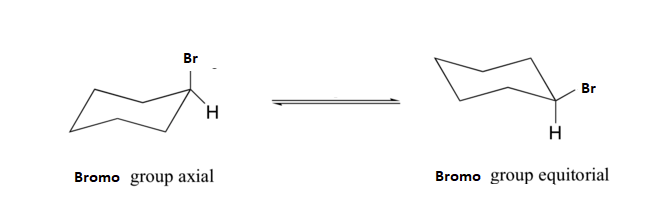
2) Calculate the energy difference between the axial and equatorial conformations of bromocyclohexane?
3) Using your answer from Question 2) estimate the percentages of axial and equatorial conformations of bromocyclohexane at 25o C.
4) There very little in 1,3-diaxial strain when going from a methyl substituent (3.8 kJ/mol) to an ethyl substituent (4.0 kJ/mol), why? It may help to use molecular model to answer this question.
Solutions
1) The ethyne group is linear and therefore does not affect the hydrogens in the 1,3 positions to say to the extent as a bulkier or a bent group (e.g. ethene group) would. This leads to less of a strain on the molecule.
2) The equatorial conformation of bromocyclohexane will have two 1,3 diaxial interactions. The table above states that each interaction accounts for 1.2 kJ/mol of strain. The total strain in equatorial bromocyclohexane will be 2(1.2 kJ/mol) = 2.4 kJ/mol.
3) Remembering that the axial conformation is higher in energy, the energy difference between the two conformations is ΔE = (E equatorial – E axial) = (0 – 2.4 kJ/mol) = -2.4 kJ/mol. After converting oC to Kelvin and kJ/mol to J/mol we can use the equation ΔE = -RT lnK to find that -ΔE/RT = lnK or (2.4 x 103 J/mol) / (8.313 kJ/mol K • 298 K) = lnK. From this we calculate that K = 2.6. Because the ring flip reaction is an equilibrium we can say that K = [Equatorial] / [Axial]. If assumption is made that [Equatorial] = X then [Axial] must be 1-X. Plugging these values into the equilibrium expression produces K = [X] / [1-X]. After plugging in the calculated value for K, X can be solved algebraically. 2.6 = [X] / [1-X] → 2.6 – 2.6X = X → 2.6 = 3.6X → 2.6/3.6 = X = 0.72. This means that bromocyclohexane is in the equatorial position 72% of the time and in the axial position 28% of the time.

4) The fact that C-C sigma bonds can freely rotate allows the ethyl subsistent to obtain a conformation which places the bulky CH3 group away from the cyclohexane ring. This forces the ethyl substituent to have only have 1,3- diaxial interactions between hydrogens, which only provides a slight difference to a methyl group.
Exercises
After completing this section, you should be able to use conformational analysis to determine the most stable conformation of a given disubstituted cyclohexane.
Make certain that you can define, and use in context, the key term below.
- conformational analysis
When faced with the problem of trying to decide which of two conformers of a given disubstituted cyclohexane is the more stable, you may find the following generalizations helpful.
- A conformation in which both substituents are equatorial will always be more stable than a conformation with both groups axial.
- When one substituent is axial and the other is equatorial, the most stable conformation will be the one with the bulkiest substituent in the equatorial position. Steric bulk decreases in the order
tert-butyl > isopropyl > ethyl > methyl > hydroxyl > halogens
Monosubstituted Cyclohexanes
In the previous section, it was stated that the chair conformation in which the methyl group is equatorial is more stable because it minimizes steric repulsion, and thus the equilibrium favors the more stable conformer. This is true for all monosubstituted cyclohexanes. The chair conformation which places the substituent in the equatorial position will be the most stable and be favored in the ring flip equilibrium.
Disubstituted Cyclohexanes
Determining the more stable chair conformation becomes more complex when there are two or more substituents attached to the cyclohexane ring. To determine the stable chair conformation, the steric effects of each substituent, along with any additional steric interactions, must be taken into account for both chair conformations.
In this section, the effect of conformations on the relative stability of disubstituted cyclohexanes is examined using the two principles:
- Substituents prefer equatorial rather than axial positions in order to minimize the steric strain created of 1,3-diaxial interactions.
- The more stable conformation will place the larger substituent in the equatorial position.
1,1-Disubstituted Cyclohexanes
The more stable chair conformation can often be determined empirically or by using the energy values of steric interactions previously discussed in this chapter. Note, in some cases there is no discernable energy difference between the two chair conformations which means they are equally stable.
1,1-dimethylcyclohexane does not have cis or trans isomers, because both methyl groups are on the same ring carbon. Both chair conformers have one methyl group in an axial position and one methyl group in an equatorial position giving both the same relative stability. The steric strain created by the 1,3-diaxial interactions of a methyl group in an axial position (versus equatorial) is 7.6 kJ/mol (from Table 4.7.1), so both conformers will have equal amounts of steric strain. Thus, the equilibrium between the two conformers does not favor one or the other. Note, that both methyl groups cannot be equatorial at the same time without breaking bonds and creating a different molecule.
However, if the two groups are different, as in 1-tert-butyl-1-methylcyclohexane, then the equilibrium favors the conformer in which the larger group (tert-butyl in this case) is in the more stable equatorial position. The energy cost of having one tert-butyl group axial (versus equatorial) can be calculated from the values in table 4.7.1 and is approximately 22.8 kJ/mol. The conformer with the tert-butyl group axial is approximately 15.2 kJ/mol (22.8 kJ/mol – 7.6 kJ/mol) less stable then the conformer with the tert-butyl group equatorial. Solving for the equilibrium constant K shows that the equatorial is preferred about 460:1 over axial. This means that 1-tert-butyl-1-methylcyclohexane will spend the majority of its time in the more stable conformation, with the tert-butyl group in the equatorial position.
Cis and trans stereoisomers of 1,2-dimethylcyclohexane
In cis-1,2-dimethylcyclohexane, both chair conformations have one methyl group equatorial and one methyl group axial. As previously discussed, the axial methyl group creates 7.6 kJ/mol of steric strain due to 1,3-diaxial interactions. It is important to note, that both chair conformations also have an additional 3.8 kJ/mol of steric strain created by a gauche interaction between the two methyl groups. Overall, both chair conformations have 11.4 kJ/mol of steric strain and are of equal stability.
In trans-1,2-dimethylcyclohexane, one chair conformer has both methyl groups axial and the other conformer has both methyl groups equatorial. The conformer with both methyl groups equatorial has no 1,3-diaxial interactions however there is till 3.8 kJ/mol of strain created by a gauche interaction. The conformer with both methyl groups axial has four 1,3-Diaxial interactions which creates 2 x 7.6 kJ/mol (15.2 kJ/mol) of steric strain. This conformer is (15.2 kJ/mol -3.8 kJ/mol) 11.4 kJ/mol less stable than the other conformer. The equilibrium will therefore favor the conformer with both methyl groups in the equatorial position.
Cis and trans stereoisomers of 1,3-dimethylcyclohexane
A similar conformational analysis can be made for the cis and trans stereoisomers of 1,3-dimethylcyclohexane. For cis-1,3-dimethylcyclohexane one chair conformation has both methyl groups in axial positions creating 1,3-diaxial interactions. The other conformer has both methyl groups in equatorial positions thus creating no 1,3-diaxial interaction. Because the methyl groups are not on adjacent carbons in the cyclohexane rings gauche interactions are not possible. Even without energy calculations it is simple to determine that the conformer with both methyl groups in the equatorial position will be the more stable conformer.
For trans-1,3-dimethylcyclohexane both conformations have one methyl axial and one methyl group equatorial. Each conformer has one methyl group creating a 1,3-diaxial interaction so both are of equal stability.
Summary of Disubstitued Cyclohexane Chair Conformations
When considering the conformational analyses discussed above a pattern begins to form. There are only two possible relationships which can occur between ring-flip chair conformations:
1) AA/EE: One chair conformation places both substituents in axial positions creating 1,3-diaxial interactions. The other conformer places both substituents in equatorial positions creating no 1,3-diaxial interactions. This diequatorial conformer is the more stable regardless of the substituents.
2) AE/EA: Each chair conformation places one substituent in the axial position and one substituent in the equatorial position. If the substituents are the same, there will be equal 1,3-diaxial interactions in both conformers making them equal in stability. However, if the substituents are different then different 1,3-diaxial interactions will occur. The chair conformation which places the larger substituent in the equatorial position will be favored.
| Substitution type | Chair Conformation Relationship |
| cs-1,2-disubstituted cyclohexanes | AE/EA |
| trans-1,2-disubstituted cyclohexanes | AA/EE |
| cis-1,3-disubstituted cyclohexanes | AA/EE |
| trans-1,3-disubstituted cyclohexanes | AE/EA |
| cis-1,4-disubstituted cyclohexanes | AE/EA |
| trans-1,4-disubstituted cyclohexanes | AA/EE |
For cis-1-chloro-4-methylcyclohexane, draw the most stable chair conformation and determine the energy difference between the two chair conformers.
Solution
Based on the table above, cis-1,4-disubstitued cyclohexanes should have two chair conformations each with one substituent axial and one equatorial. Based on this, we can surmise that the energy difference of the two chair conformations will be based on the difference in the 1,3-diaxial interactions created by the methyl and chloro substituents.
As predicted, each chair conformer places one of the substituents in the axial position. Because the methyl group is larger and has a greater 1,3-diaxial interaction than the chloro, the most stable conformer will place it the equatorial position, as shown in the structure on the right. Using the 1,3-diaxial energy values given in the previous sections we can calculate that the conformer on the right is (7.6 kJ/mol – 2.0 kJ/mol) 5.6 kJ/mol more stable than the other.
For trans-1-chloro-2-methylcyclohexane, draw the most stable chair conformation and determine the energy difference between the two chair conformers.
Solution
Based on the table above, trans-1,2-disubstitued cyclohexanes should have one chair conformation with both substituents axial and one conformation with both substituents equatorial. Based on this, we can predict that the conformer which places both substituents equatorial will be the more stable conformer. The energy difference of the two chair conformations will be based on the 1,3-diaxial interactions created by both the methyl and chloro substituents.
As predicted, one chair conformer places both substituents in the axial position and other places both substituents equatorial. The more stable conformer will place both substituents in the equatorial position, as shown in the structure on the right. Using the 1,3-diaxial energy values given in the previous sections we can calculate that the conformer on the right is (7.6 kJ/mol + 2.0 kJ/mol) 9.6 kJ/mol more stable than the other.
Conformational Analysis of Complex Six Membered Ring Structures
Cyclohexane can have more than two substituents. Also, there are multiple six membered rings which contain atoms other than carbon. All of these systems usually form chair conformations and follow the same steric constraints discussed in this section. Because the most commonly found rings in nature are six membered, conformational analysis can often help in understanding the usual shapes of some biologically important molecules. In complex six membered ring structures a direct calculation of 1,3-diaxial energy values may be difficult. In these cases a determination of the more stable chair conformer can be made by empirically applying the principles of steric interactions.
A later chapter will discuss how many sugars can exist in cyclic forms which are often six remembered rings. When in an aqueous solution the six carbon sugar, glucose, is usually a six membered ring adopting a chair conformation. When looking at the two possible ring-clip chair conformations, one has all of the substituents axial and the other has all the substutents equatorial. Even without a calculation, it is clear that the conformation with all equatorial substituents is the most stable and glucose will most commonly be found in this conformation.
The six carbon sugar, fructose, in aqueous solution is also a six-membered ring in a chair conformation. Which of the two possible chair conformations would be expected to be the most stable?
Solution
The lower energy chair conformation is the one with three of the five substituents (including the bulky –CH2OH group) in the equatorial position (pictured on the right). The left structure has 3 equatorial substituents while the structure on the right only has two equatorial substituents.
Exercises
1. Draw the two chair conformations for cis-1-ethyl-2-methylcyclohexane using bond-line structures and indicate the more energetically favored conformation.
2. Draw the most stable conformation for trans-1-ethyl-3-methylcyclohexane using bond-line structures.
3. Draw the most stable conformation for trans-1-t-butyl-4-methylcyclohexane using bond-line structures.
4. Draw the most stable conformation fo trans-1-isopropyl-3-methylcyclohexane.
5. Can a ‘ring flip’ change a cis-disubstituted cyclohexane to trans? Explain.
6. Draw the two chair conformations of the six-carbon sugar mannose, being sure to clearly show each non-hydrogen substituent as axial or equatorial. Predict which conformation is likely to be more stable, and explain why.

Solutions



4.

The bulkier isopropyl groups is in the equatorial position.
5. No. In order to change the relationship of two substituents on a ring from cis to trans, you would need to break and reform two covalent bonds. Ring flips involve only rotation of single bonds.
6.

Exercises
Find the word

