7.1.3: Describing Chemical Bonds – Valence Bond Theory
After completing this section, you should be able to
- explain how covalent bonds are formed as a result of the ability of atoms to share electrons.
- describe the formation of covalent bonds in terms of the overlapping of atomic orbitals.
Make certain that you can define, and use in context, the key terms below.
- bond strength
- covalent bond
- bond length
- sigma (σ) bond
- pi (π) bond
- valence bond theory
Valence Bond Theory
As we have been discussing how to use Lewis structures to depict the bonding in organic compounds, we have been very vague so far in our language about the actual nature of the chemical bonds themselves. We know that a covalent bond involves the ‘sharing’ of a pair of electrons between two atoms – but how does this happen, and how does it lead to the formation of a bond holding the two atoms together? Two main models have been developed to described how covalent bonds are formed: valence bond theory and molecularly orbital theory.
Valence bond theory is most often used to describe bonding in organic molecules. In this model, covalent bonds are considered to form from the overlap of two atomic orbitals on different atoms, each orbital containing a single electron. The electrons become paired in the orbital overlap bonding the atoms together.
The simplest example valence bond theory can be demonstrated by the H2 molecule. We can see from the periodic table that each hydrogen atom has a single valence electron. If 2 hydrogen atoms come together to form a bond, then each hydrogen atom effectively has a share in both electrons and thus each resembles the noble gas helium and is more stable. The 2 electrons shared in the orbital overlap are represented by a single dash between the atoms.

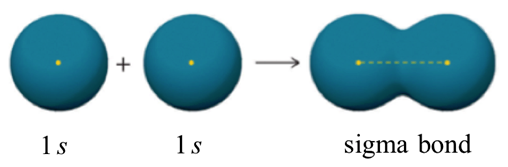
Valence bond theory describes a chemical bond as the overlap of atomic orbitals. In the case of the hydrogen molecule, the 1s orbital of one hydrogen atom overlaps with the 1s orbital of the second hydrogen atom to form a molecular orbital called a sigma bond which contains two electrons of opposite spin. The mutual attraction between this negatively charged electron pair and the two atoms’ positively charged nuclei serves to physically link the two atoms through a force we define as a covalent bond. The strength of a covalent bond depends on the extent of overlap of the orbitals involved. Orbitals that overlap extensively form bonds that are stronger than those that have less overlap.
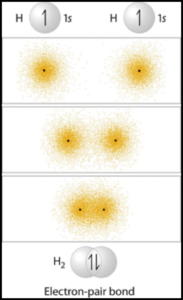
ne more characteristic of the covalent bond in H2 is important to consider at this point. The two overlapping 1s orbitals can be visualized as two spherical balloons being pressed together. This means that the bond has cylindrical symmetry: if we were to take a cross-sectional plane of the bond at any point, it would form a circle. This type of bond is referred to as a σ(sigma) bond.
The energy of the system depends on how much the orbitals overlap. The energy diagram below illustrates how the sum of the energies of two hydrogen atoms (the colored curve) changes as they approach each other. When the atoms are far apart there is no overlap, and by convention we set the sum of the energies at zero. As the atoms move together, their orbitals begin to overlap. Each electron begins to feel the attraction of the nucleus in the other atom. In addition, the electrons begin to repel each other, as do the nuclei. While the atoms are still widely separated, the attractions are slightly stronger than the repulsions, and the energy of the system decreases. (A bond begins to form.) As the atoms move closer together, the overlap increases, so the attraction of the nuclei for the electrons continues to increase (as do the repulsions among electrons and between the nuclei). At some specific distance between the atoms, which varies depending on the atoms involved, the energy reaches its lowest (most stable) value. This optimum distance between the two bonded nuclei is called the the bond lengths between the two atoms. The bond is stable because at this point, the attractive and repulsive forces combine to create the lowest possible energy configuration.
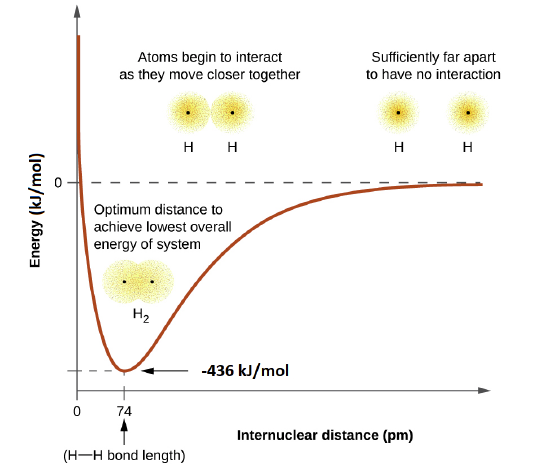
This optimal internuclear distance is the bond length. For the H2 molecule, the distance is 74 pm (picometers, 10-12 meters). Likewise, the difference in potential energy between the lowest energy state (at the optimal internuclear distance) and the state where the two atoms are completely separated is called the bond dissociation energy, or, more simply, bond strength. For the hydrogen molecule, the H-H bond strength is equal to about 435 kJ/mol. This means it would take 435 kJ to break one mole of H-H bonds.
Every covalent bond in a given molecule has a characteristic length and strength. In general, the length of a typical carbon-carbon single bond in an organic molecule is about 150 pm, while carbon-carbon double bonds are about 130 pm, carbon-oxygen double bonds are about 120 pm, and carbon-hydrogen bonds are in the range of 100 to 110 pm. The strength of covalent bonds in organic molecules ranges from about 234 kJ/mol for a carbon-iodine bond (in thyroid hormone, for example), about 410 kJ/mole for a typical carbon-hydrogen bond, and up to over 800 kJ/mole for a carbon-carbon triple bond.
| Bond | Length (pm) | Energy (kJ/mol) | Bond | Length (pm) | Energy (kJ/mol) | |
|---|---|---|---|---|---|---|
| H-H | 74 | 436 | C-O | 140.1 | 358 | |
| H-C | 106.8 | 413 | C=O | 119.7 | 745 | |
| H-N | 101.5 | 391 | C≡O | 113.7 | 1072 | |
| H-O | 97.5 | 467 | H-Cl | 127.5 | 431 | |
| C-C | 150.6 | 347 | H-Br | 141.4 | 366 | |
| C=C | 133.5 | 614 | H-I | 160.9 | 298 | |
| C≡C | 120.8 | 839 | O-O | 148 | 146 | |
| C-N | 142.1 | 305 | O=O | 120.8 | 498 | |
| C=N | 130.0 | 615 | F-F | 141.2 | 159 | |
| C≡N | 116.1 | 891 | Cl-Cl | 198.8 | 243 |
Exercises
1) For the following energy diagram for energy vs. intermolecular distance is for a fluorine molecule (F2). Please describe the importance for points A, B, & C on the graph.
Solutions
1)
A – Repulsive Forces are present, nuclei are too close to one another.
B – Optimal distance between the two orbitals to have a bond (the bond length)
C – Cannot form a bond, the orbitals are too far apart.
Crosswords

